While I've been underway working on the C# Networking tutorial series I've been doing quite a few site updates.  It's given me a chance to add some Dart code to the site and I've decided to share some of the little playthings that I make with it.  You can find them over here.  It's not supposed to be a rational tutorial/walkthrough; nothing builds upon itself.  They are one-shot samples.  I don't plan on regularly updating it, just when I want to.

I've been a little bored while waiting for the parts and tools to come in for my January project. After playing Fez and trying out the stereoscopy mode, I decided to pass the time by trying to add the feature to my 3D cube.

Stereoscopy works by creating two cameras, one for the right eye and one for the left. These two cameras are a small distance apart. Each of them will see a slight different image/projection of the 3D objects. An image from anSGI tutorial written by Paul Bourke gives a great visualization:

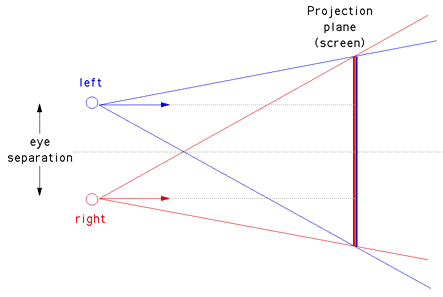
There are multiple ways to view the right and left images. Probably the most common is the use of red and cyan filters. Though systems like the RealD 3D use polarized light to achieve this effect. The first method has significant color quality loss on images, where as the later has much less loss. The reason why the first method is much more prevalent is that it is much cheaper and easier to do. E.g., it doesn't require any extra equipment (sans the glasses) and is not to difficult to implement. Systems like Nintendo's 3DS use a phenomenon known as Autosteroscopy that doesn't require glasses, this is achieved by having Lenticular Lenses applied to the display. It's pretty nifty, and the quality isn't too bad, but there is there are the slight problems that it is more expensive and the viewer need to be in a “sweet spot,” to see the 3D image.

I decided to go with the red/cyan image method. In the current state of my 3D cube program, I don't have anything complicated like cameras added in, so to get this working I did this:

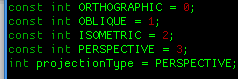
p = a perspective projected line
q = an oblique projection on p,
    with theta = PI / 180, and a small skew value on the x component
r = an oblique projection on p,
    with theta = PI, and a small skew value on the x component
color q with blue
color r with red
draw q
draw r

It's definitely an improper method, NEVER DO THIS, but it does give off the effect. I updated the repo page in case you want to view the source. Just change the variable renderStereo to be true.

Below is the stereo-scoped 3D cube (as JavaScript)

Finals are over and I'm back at home now.  I haven't really had a nice long break in the past 2-3 years, so I'm really looking forward to these next five weeks.  I'm currently waiting for from stuff from Amazon to work on my project for the break (I'll make a separate post later).

In the mean time, I decided to take a look into Google's JavaScript replacement; Dart.  So far, I've really liked it.  I did the Pirate Badge tutorial, but to really get into it, I went ahead and ported my 3D Canvas Cube to the language.  There were also some improvements.  Addition of a perspective view, better scaling, and fixing a bug where I was drawing an Impossible Cube.

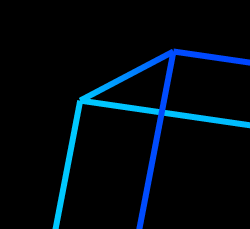
When the line width of the cube was at the size of "1," it's pretty hard to see, but when you scale up the size, it's clearly visible.  To fix this, I employed a simple algorithm:

sortedLines = List of "Line," objects
zLineMap = Key-Value map of floating points and a List of "Line," objects
For each line:
  Look at the z coordinates of each endpoint of the line
  zMin = Take the lesser of the two z's
  
  If zMin is a key already in zLineMap:
    Append it to the List at zLineMap[zMin]
  Else:
    Create a new list containing only the line
    Add it to zLineMap at key zMin (i.e. zLineMap[zMin])

zKeys = sorted List of the keys in zLineMap (ascending)
i = 0
For each key in zKeys:
  For each line in zLineMap[key]:
    Put the line into sortedLines at i (i.e. sortedLines[i] = line)
    increment i by 1

This algorithm might not be the most efficient (mostly likely because I haven't formally studied any computer graphics), but it avoids the issue of accidentally drawing an impossible cube.  This bug was happening because I had an array of lines, would apply a rotation "matrix," to them, then sent them off to be drawn.  The drawing function would process them in the order that they were indexed.  Sometimes it would look right, but most of the time it would not.

The rotating cube that you see in this post had been compiled to JavaScript with the dart2js tool.  If you want to see the source, it's in my toybox repo here.  Don't forget the accompying HTML page.