In the realm of computer science, we're always told to pursue what is the most efficient solution. This can be either what is the fastest way to solve a problem; or what may be the cheapest.

What is the easiest, but not always the best, is typically a "greedy algorithm"; think bubble sort. More often than not, there is a much more efficient method which typically involves thinking about the problem a bit deeper. These are often the analytical solutions.

Whilst working on PSRayTracing (PSRT), I was constantly finding inefficient algorithms and data structures. There are places where it was obvious to improve something, whereas other sections really needed a hard look-at to see if there was more performance that could be squeezed out. After the podcast interview I was looking for the next topic to cover. Scanning over older code, I looked at the random number generator since it's used quite a bit. I spotted an infinite loop and thought "there has to be something better".

The code in question is a method to generate a 2D (or 3D) vector, which falls within a unit circle (or sphere). This is the algorithm that the book originally gave us:

Vec3 get_in_unit_disk() {
    while (true) {
        const Vec3 p(get_real(-1, 1), get_real(-1, 1), 0);
        if (p.length_squared() >= 1)
            continue;

        return p;
    }
}

The above in a nutshell:

1. Generate two (random) numbers between [-1.0, 1.0] to make a (2D) vector
2. If the length squared of the vector is 1 or greater, do step 1 again
3. If not, then you have a vector that's within the unit circle

(The 3D case is covered by generating three numbers at step 1)

 

This algorithm didn't feel right to me. It has some of that yucky stuff we hate: infinite looping and try-and-see-if-it-works logic. This could easily lead to branch prediction misses, being stuck (theoretically) spinning forever, wasting our random numbers. And it doesn't feel "mathematically elegant".

My code had some commented out blocks with an analytical solution to the above. But in the years prior when I had first touched that code I had left a note saying that it was a bit slower than using the loop.

The next day I had an email fall into my inbox. It was from GitHub notifying me of a response. The body was about how to generate a random point inside of a unit sphere... Following the link to the discussion, it came from the original book's repository. The first reply in 4 years on a topic... that... I... created...

I think this was a sign from above to investigate it again.

 

Reading through the old discussion ^{(please don't look I'm embarrassed)}, one of the maintainers @hollasch left a good comment:

What really stuck out to me is in the beginning:

"The current approach is significantly faster in almost all cases than any analytical method so far proposed ... every time our random sampling returns an answer faster than the analytical approach,"

Are rejection methods much faster than an analytical solution? Huh.

 

Understanding The Problem A Little More

As seen above, there is an analytical solution to the above algorithm for both the 2D and 3D cases. We'll use Python for the moment.

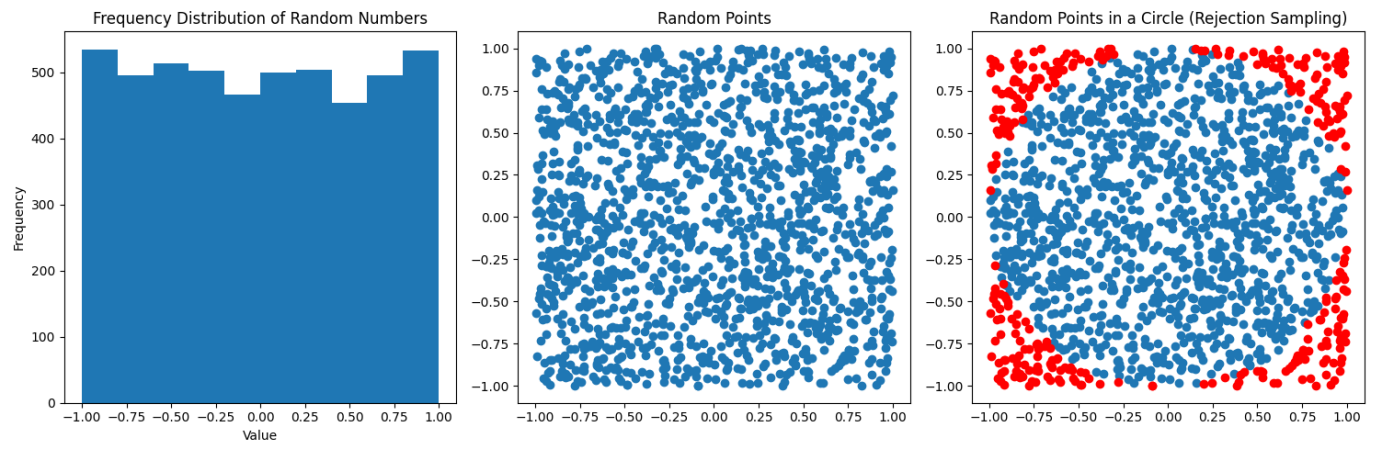
In the above diagrams, we're just taking a random sampling of points inside a 2D plane. You can see they are fairly uniformly distributed. To the far right the points in blue are what falls within the unit circle, the red is what falls outside (and we must throw out). In a nutshell this is a visualization of the rejection sampling method:

def rejection_in_unit_disk():
   while True:
       x = random.uniform(-1, 1)
       y = random.uniform(-1, 1)
       v = Vec2(x, y)

       if (v.length_squared() < 1):
           return v

 

Using the area formulas for a square and a circle, we can find out the chance that a point will fall inside the circle:

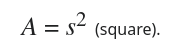
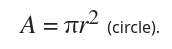
In this case, r = s / 2, and it's <circle area> / <square area>. If you do all of the math, you'll find that the odds are ~78.54%. Which means that around 22% of our points are rejected; that isn't desirable.

For the analytical solution, you have to think in terms of polar coordinates: Generate a random radius and generate a random angle. Initially you might assume the correct method is this:

def analytical_in_unit_disk_incorrect():
   r = random.uniform(0, 1)
   theta = random.uniform(0, two_pi)
   x = r * math.cos(theta)
   y = r * math.sin(theta)

   return Vec2(x, y)

 

But that's not quite right:

 

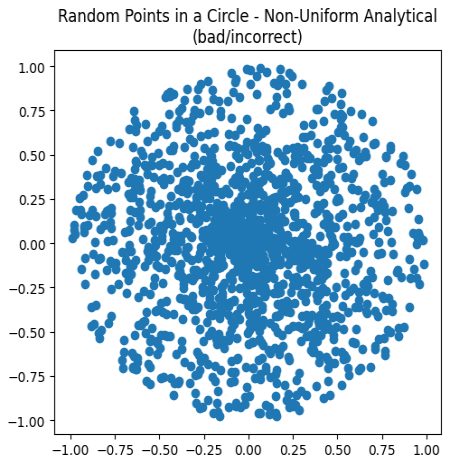
Charting these points, while all are falling within the unit circle, they are clustering more in the center. This is not correct. We need to alter the distribution of the points to appear more uniform. Remember from math class how you needed to use a square root to calculate the distance of a vector? That's also the trick to fixing the scattering:

def analytical_in_unit_disk():
   r = math.sqrt(random.uniform(0, 1))
   theta = random.uniform(0, two_pi)
   x = r * math.cos(theta)
   y = r * math.sin(theta)

   return Vec2(x, y)

 

Huzzah! We now have the analytical solution:

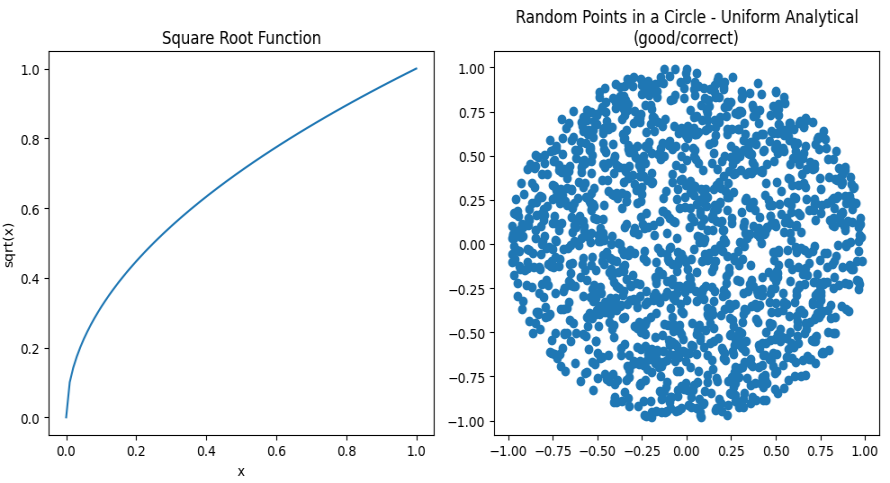
Look at how beautiful that is:

1. All points fall within the unit circle
2. All look to be equally distributed
3. No (theoretical) infinite looping
4. No wasted random numbers

The 3D case the rejection method is the same (but you add an extra Z-axis).

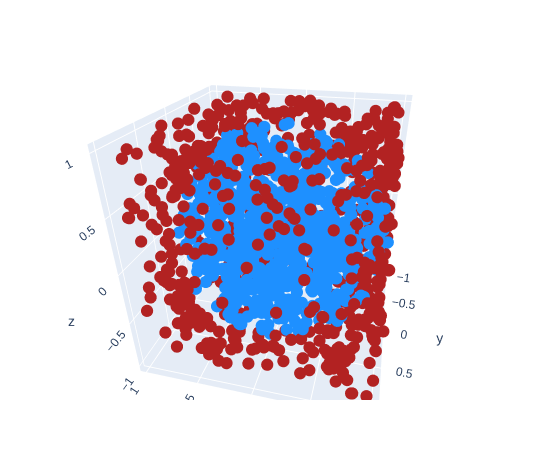
How much more inefficient is the rejection sampling in 3D? It's way worse than the 2D case. Take these volume formulas. The first being that of a cube's and the second that of a sphere's.

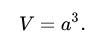
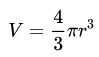
Similarly, when a = r / 2, the chance a randomly generated point (using rejection sampling) falls within the sphere, is only 52.36%. You have to throw out nearly half of your points!

The analytical (spherical) method is a tad more complex, but it follows the same logic. If you want to read more about this, Karthik Karanth wrote an excellent article. The Python code for the 3D analytical solution is as follows:

def analytical_in_unit_sphere():
   r = math.cbrt(random.uniform(0, 1))
   theta = random.uniform(0, two_pi)
   phi = math.acos(random.uniform(-1, 1))

   sin_theta = math.sin(theta)
   cos_theta = math.cos(theta)
   sin_phi = math.sin(phi)
   cos_phi = math.cos(phi)

   x = r * sin_phi * cos_theta
   y = r * sin_phi * sin_theta
   z = r * cos_phi

   return Vec3(x, y, z)

 

Jumping ahead in time just a little, let me show you the same scene rendered twice over, but with each different sampling method:

 

The one on the left was using boring rejection sampling, whereas the one on the right is using this new fancy analytical method. At a first glance the two images are indistinguishable; we'd call this "perceptually the same". Zooming in on a 32x32 patch of pixels (in the same location) you can start to spot some differences.  This is because we are now traversing through our random number generator differently with these two methods.  It alters the fuzz, but for the end user it is the same image.

_{(Hint: look at the top two rows, especially the purple near the right side)}

 

Benchmarking (Part 1)

Let's stay in Python land for the moment because it's easier. We can create a small benchmark to see how long it takes to generate both the 2D & 3D points. The full source code of the program can be found here. The critical section is this:

# Returns how many seconds it took
def measure(rng_seed, num_points, method):
   bucket = [None] * num_points  # preallocate space

   random.seed(rng_seed)

   start_time = time.time()
   for i in range(0, num_points):
       bucket[i] = method()
   end_time = time.time()

   return (end_time - start_time)


def main():
   rng_seed = 1337
   num_runs = 500
   num_points = 1000000

   # ...

   for i in range(0, num_runs):
       seed = rng_seed + i

       r2d = measure(seed, num_points, rejection_in_unit_disk)
       a2d = measure(seed, num_points, analytical_in_unit_disk)
       r3d = measure(seed, num_points, rejection_in_unit_sphere)
       a3d = measure(seed, num_points, analytical_in_unit_sphere)

       # ...

 

From there we can take measurements of how long each method took and compare them. Running on a 10th Gen i7 (under Linux), this is the final runtime of the benchmark:

Rejection 2D:
  Mean: 0.893 s
  Median: 0.893 s
Analytical 2D:
  Mean: 0.785 s
  Median: 0.786 s
Rejection 3D:
  Mean: 1.559 s
  Median: 1.560 s
Analytical 3D:
  Mean: 1.151 s
  Median: 1.150 s

 

Looking at the median rejection sampling is 13% slower in the 2D case and 35% in the 3D case!! Surely, we must now use the analytical method. All of this work we've done was definitely worth it!

 

Taking It Into The Ray Tracer

Placing the analytical methods into the ray tracer was very trivial. All of the math functions exist in the standard library therefore the port from Python is nearly 1-1 one to one. Here's how long it takes to the render the default scene with the sad-poor rejection sampling:

me@machine:$ ./PSRayTracing -j 4 -n 500 -o with_rejection.png
...
Render took 105.956 seconds

 

And now, recompiled with our Supreme analytical method:

me@machine:$ ./PSRayTracing -j 4 -n 500 -o with_analytical.png
...
Render took 118.408 seconds

^{(These measurements were taken with the same 10th Gen i7 on Linux compiled with GCC 14 using CMake's Release mode.)}

Wait, it took longer to use the analytical method?  Inspecting both renders they are perceptually the same. Pixel for pixel there are differences, but this is expected because the random number generator is being used differently now.

Just like my note from 4 years ago said... It's... Slower... Something Ain't Right.

 

Benchmarking (Part 2)

We need to dig in a little more here. Let's benchmark the four methods separate from the ray tracer again, but this time in C++. If you want to read the source, I'll leave the link right here: comparing_greedy_vs_analytical.cpp . It's structured a tiny bit different from the Python code, but we have as little overhead as possible. We'll also be using the same RNG engine, the Mersenne Twister (MT).

I want to take an aside here to mention that PSRT actually uses PCG by default for random number generation. It's much more performant than the built in MT engine and doesn't get exhausted as quickly. I wrote about it briefly before. The MT engine can be swapped back in if so desired. While any random number generation method can greatly impact performance, in this case it is not the cause of the slowdown seen above.

me@machine:$ g++ comparing_greedy_vs_analytical.cpp -o test
./test 1337 500 1000000
Testing with 1000000 points, 500 times...
run_number: rejection_2d_ms, analytical_2d_ms, rejection_3d_ms, analytical_3d_ms
1: 516, 268, 658, 423,
2: 295, 273, 640, 428,
...
499: 306, 278, 670, 445,
500: 305, 279, 676, 446,

mean: 313, 277, 675, 448
median: 305, 276, 665, 444
(all times measured are in milliseconds)

 

It's still showing the analytical method is still much more faster than the rejection sampling. About 10% for 2D and nearly 33% for 3D. Which is what is aligned with the Python benchmark. What could be going on here...  Oh wait; Silly me...

I forgot to turn on compiler optimizations... Let's run this again now!

me@machine:$ g++ comparing_greedy_vs_analytical.cpp -o test -O3
./test 1337 500 1000000
Testing with 1000000 points, 500 times...
run_number: rejection_2d_ms, analytical_2d_ms, rejection_3d_ms, analytical_3d_ms
1: 87, 137, 96, 81,  
2: 17, 33, 40, 80,  
...
499: 18, 35, 42, 82,  
500: 18, 35, 44, 82,  

mean: 20, 38, 44, 82
median: 17, 34, 42, 82
(all times measured are in milliseconds)

 

What-

The rejection sampling methods are faster?! And by 50%?!!?!

This needs more investigation.

 

Benchmarking (Part 3)

If you've read the other posts in this series, you know that I like to test things on every possible permutation/combination that I can think of.  At my disposal, I have:

• An Intel i7-1050H
• An AMD Ryzen 9 6900HX
• An Apple M1

With the x86_64 processors I can test GCC, clang, and MSVC. GCC+Clang on Linux and GCC+MSVC on Windows. For macOS we're playing with ARM processors so I only have Clang+GCC available. This gives us 10 different combinations of Chip+OS+Compiler to measure. But seeing above how optimizations levels affected the runtime we need to look at different compiler optimization flags (-O1, -Ofast, /Od, /Ox, etc). In total there are 48 cases which can be tested.

 

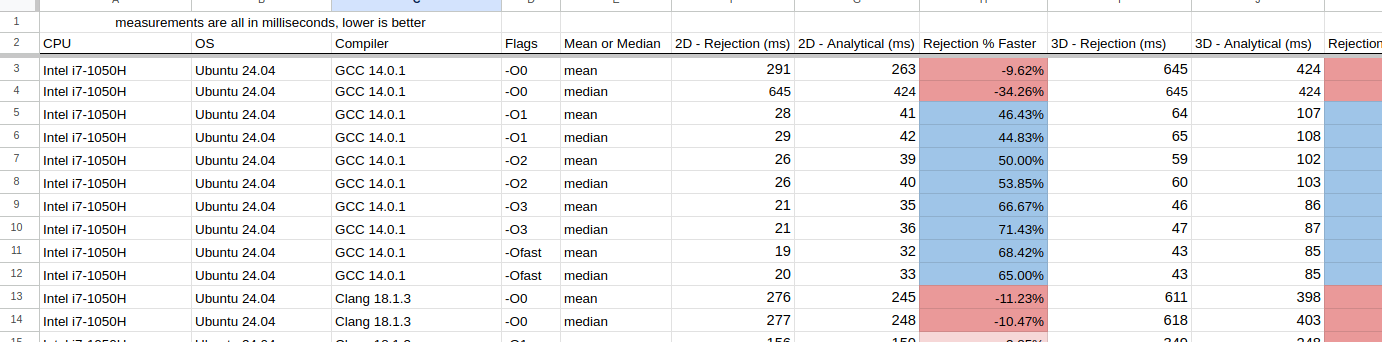
Using the above C++ benchmark, the results have been placed into a Google Sheet. As always, they yield some fascinating results:

Normally, I would include some fancy charts and graphs here, but I found it very difficult to do so and I didn't want to cause any confusion. Instead there are some interesting observations I want to note:

• For Intel+Linux+GCC just turning on -O1 yielded significant improvements
  • On average, optimizations made rejection sampling 50% faster
• For Intel+Linux+Clang in nearly all of the cases, the analytical method was faster
  • Especially for 3D
  • The only exception was when -Ofast was used, the rejection sampling performed better
• For Intel+Windows+GCC rejection sampling was always better. Typically +150% for the 2D case, and +70% for 3D
• Intel+Windows+MSVC is comparable to the above (GCC) but was slower
• On AMD, all compilers on each OS behaved the same as on Intel
• With the M1 chip (macOS) GCC performed much better than clang
  • Except for -O0 GCC's rejection sampling was always faster than the analytical method
  • Clang on the other hand, 2D rejection sampling was faster, but for the 3D case, using the analytical method was faster.

This is a bit bonkers, as I really didn't expect there to be that much difference. Clang seemed to do better with analytical sampling, but GCC (with optimizations on) using rejection sampling stole the show. In general, I'm going to claim now that rejection sampling is better to use.

 

Assembly Inspection

I'm always iffy when it comes to inspecting the assembly. It's not my wheelhouse, and playing "count the instructions" is my favorite way of measuring performance; running code with a stopwatch is. If you need a basic primer on the topic, these two videos give a nice overview about some more of the important parts:

• x86_64 jumps and control flow
• X86_64 calls

Reducing instruction counts, jumps and calls are what we aim for.

Taking a look at GCC 14.2's x86_64 output, the -O0 case is quite straightforward. We're going to only cover the 2D case as it's less to go through.

First up with rejection sampling (full code here), it will take around ~110 instructions to fully complete. Coupled with that we have 4 procedure calls and at the end a check to see if we need to repeat the entire process (and remember there is 22% chance it could happen). In the case we repeat it, then it would be around ~205 instructions (and 8 procedure calls).

In the analytical case (full code here) there's a little less than ~100 instructions to compute. Now on the flip-side there are 6 calls, but there is zero chance that we'll have to repeat anything in the procedure.

When cracking up that compiler to -O3, we have to throw everything above out the window as the assembly becomes very hard to decipher. I'll try my best, but if I'm wrong, someone who could contact me to correct it would be much appreciated

(Full code here) This is where I think the rejection method is in the code. This is because of the jne L16 line. A similar pattern of execution is viewed above for -O0. The compiler is optimizing away and inlining a bunch of other functions which makes this hard to track. Here, we have only 45 instructions to run, and not a single call!

(Full code here) This is my best guess of the -O3'd analytical method. The clue here for us is there are the two call instructions; one to sincos() and sqrt(). This looks to be about 55 instructions long, which already loses the counting competition. Coupled in with the calls this will definitely be slower.

Measuring the runtime of the code will always beat looking at assembly. The assembly can give you insights, but it's worthless in the face of a clock. And as you can see from turning on -O3 (or even -O1) it can be much harder to glean anything useful.

 

Benchmarking (Part 4)

Just because the smaller test case shows a 50%+ performance boost in some cases, that doesn't mean we'll see that same increase in the larger application. A benchmark of a small piece of code is meaningless until it's been placed into a larger application. If you've read the previous posts from this blog, this is where I like to do some exhaustive testing of the Ray Tracing code for hundreds of hours. 🫠🫠🫠

The testing methodology is simple:

1. There are 20 scenes in the ray tracer
2. We'll test each of them 50 times over with different parameters
3. The same test will be run once with rejection sampling and once with the analytical method
4. The difference in runtime will be written down

I need to note I turned on the use of the real trig functions this time. By default PSRT will use (slightly faster) trig approximations. But to better keep in line with the benchmark from above, 100% authentic-free-range-organic-gluten-free-locally-grown sin(), cos(), atan2(), etc() was used. You can read more about the approximations here.

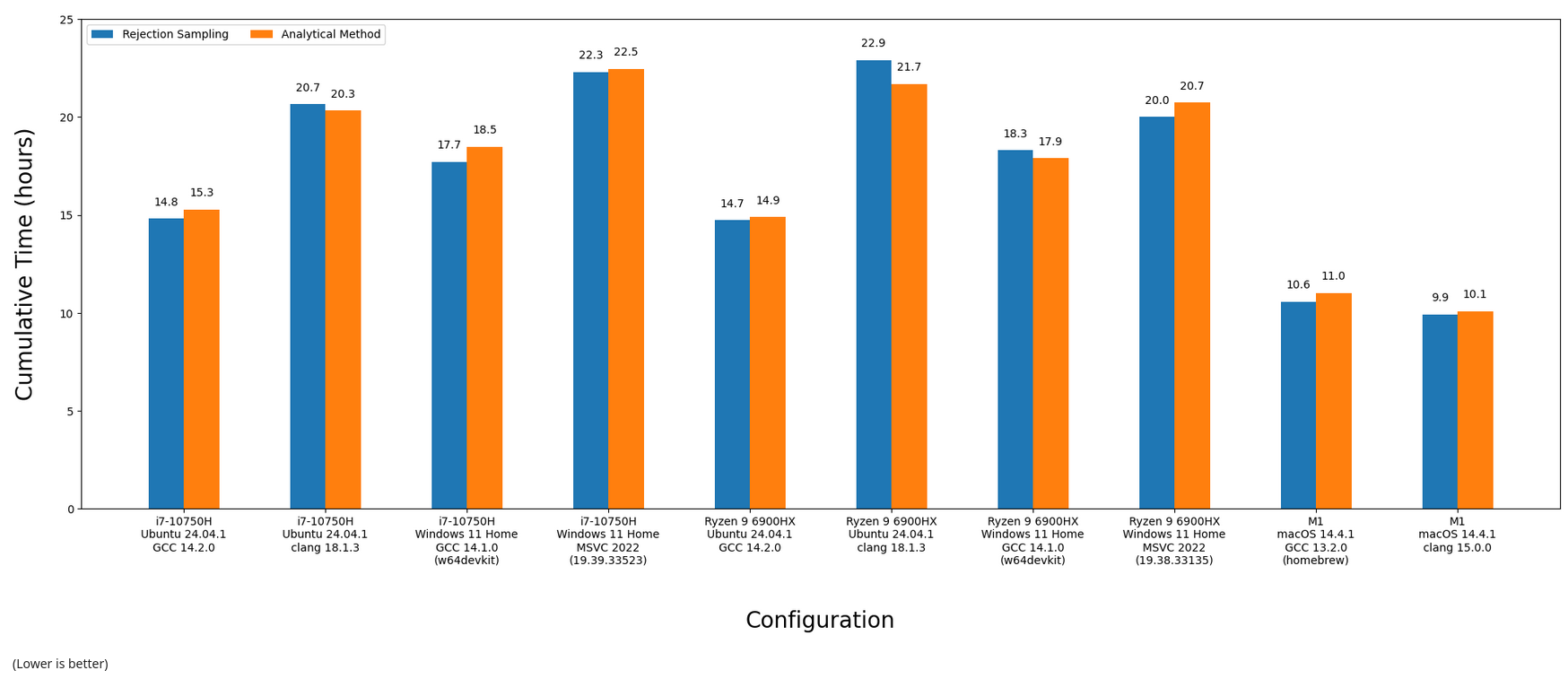
After melting all of the CPUs available to me, here are the final results. Everything was compiled in (CMake's) Release mode, which should give us the fastest code possible (e.g. -O3):

In some cases, rejection sampling was faster, in others using the analytical method was. Visualizing the above as fancy bar charts:

 

 

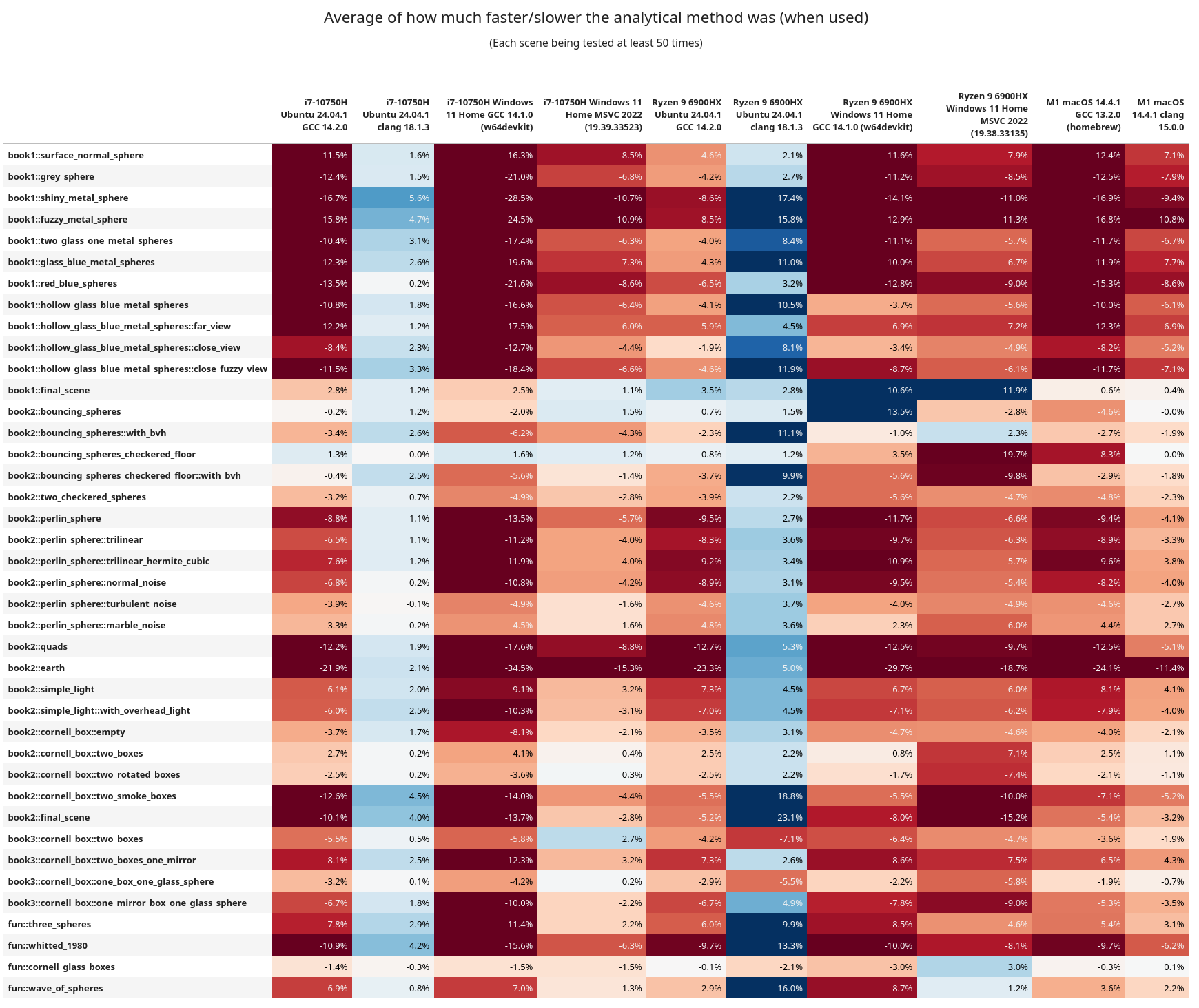
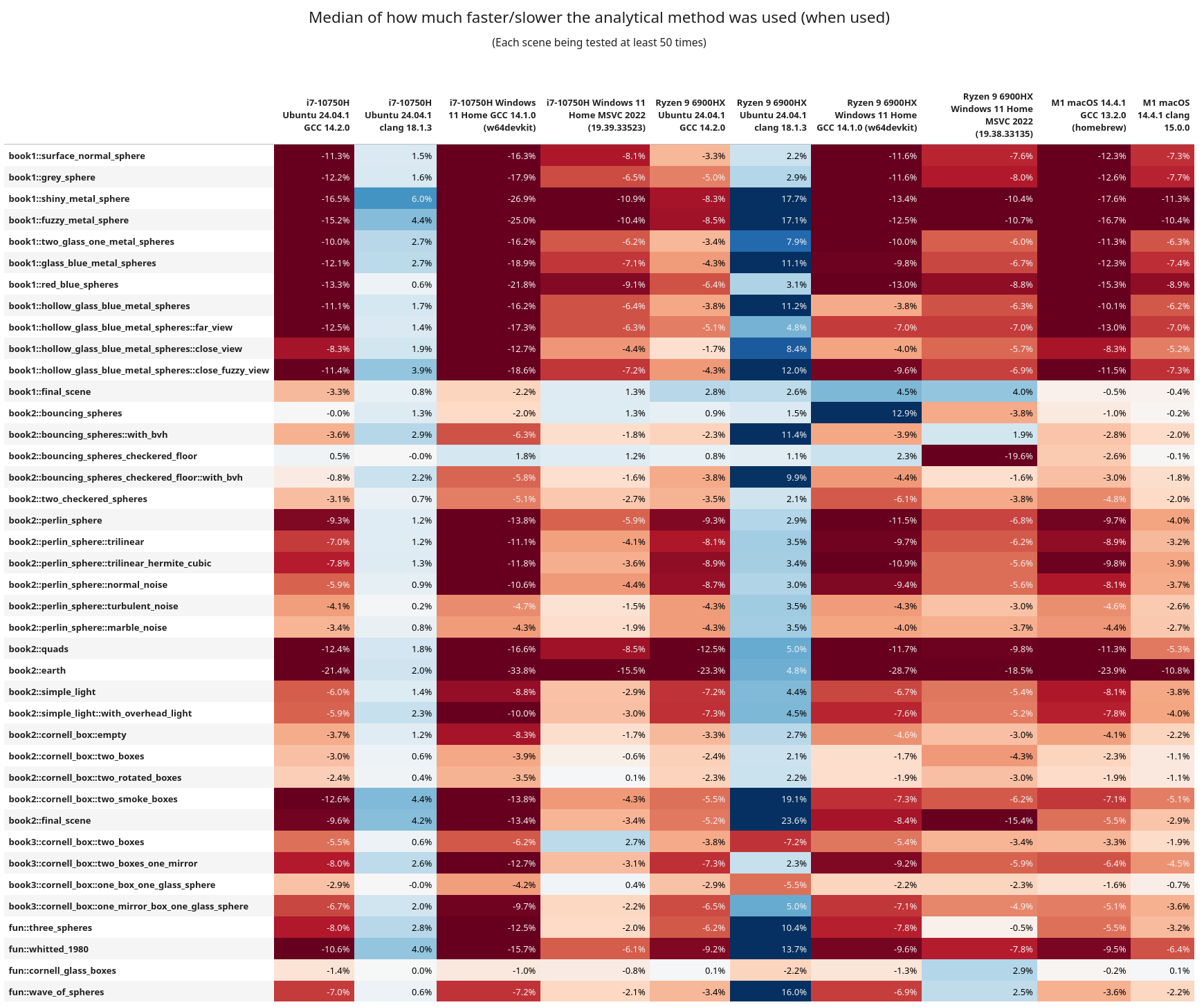
The scene by scene breakdown is more intriguing. Here's the means and medians for each scene vs. configuration:

 

Here are some of the interesting observations:

• In general, rejection sampling is MUCH more performant, and sometimes by a wide margin
• Clang was having a better time on x86_64 when using the analytical method
  • But keep in mind GCC is overall more performant, and with rejection sampling instead
• book1::final_scene and book2::bouncing_spheres have lots of elements in them, but are not using a BVH tree for ray traversal. Across the board rejection sampling isn't helping too much, and in fact the analytical method is more performant.
• After them these scenes have a with_bvh variant (that does use the BVH tree) and they then see a benefit from rejection sampling.
  • When using analytical sampling the AMD chip isn't getting hit as hard on performance as the Intel one. This is more easily observed in the book1 scenes.  Following these, all of the scenes now use a BVH tree
  • On Linux+GCC, Intel and AMD ran the entire test suite in approximately the same time, but AMD was every so slightly faster
  • Linux+Clang ran better on Intel
  • Intel+Windows+GCC had rejection faster, but AMD+Windows+GCC did better with analytical
  • AMD ran the Windows+MSVC code significantly faster (by 2 hours!!)
  • From the assembly inspection above, I wonder if maybe the AMD chips are better at running the call instruction? Or are better at running some of the math functions. This is wild guessing at this point.
  • I do want to note that these are chips from different generations, so it can be like comparing apples to oranges.

If you want to see the variance from the above tables, it's here, but it's more boring to look at.

 

Benchmarking (Part 5)

While clang was slower than GCC, it was surprising to see that it actually had a performance benefit when running the analytical method. Seeing how Python also fared better with this method, I thought it might be worth seeing what happens elsewhere. Clang is built upon LLVM, So it's possible that this could have an effect on other languages of that lineage. Let's take a trip to the Rustbelt.

To keep things as simple as possible, we're going to port the smaller C++ benchmark (not PSRT). I've tried to keep it as one-to-one as possible too. The code is nothing special, so I'll link it right here if you wish to take a look. This is the first Rust program I have ever written; please be gentle.

Running on the same Intel & Linux machine as above (using rustc v1.83), Debug (no optimizations) reported that rejection was slower and the analytical faster:

Testing with 1000000 points, 500 runs...    [rng_seed=1337]
run number: rejection_2d_ms, analytical_2d_ms, rejection_3d_ms, analytical_3d_ms
1: 216, 202, 480, 344
2: 218, 206, 475, 344
...
499: 210, 198, 454, 329
500: 209, 198, 454, 328

mean: 211, 199, 459, 332
median: 211, 199, 458, 331
(all times are measured in milliseconds)

 

And with Release turned on rejection was faster:

Testing with 1000000 points, 500 runs...    [rng_seed=1337]
run number: rejection_2d_ms, analytical_2d_ms, rejection_3d_ms, analytical_3d_ms
1: 24, 32, 49, 81
2: 19, 32, 44, 82
...
499: 19, 32, 44, 82
500: 19, 32, 44, 81

mean: 19, 31, 43, 81
median: 19, 32, 44, 82
(all times are measured in milliseconds)

 

What's fun to note here is this Rust version is slightly faster than its C++/GCC equivalent. But when the same code is compiled with C++/Clang it doesn't do as well (check rows 11, 12, 21, & 22).  I'm glad to see that Rust is exhibiting the same behavior as C++ with and without optimizations.

 

Closing Remarks

After all of this work, PSRT will stick with using the naive rejection sampling over the beautiful analytical method. It's frustrating to spend time on something you thought was the better way, only to find out that, well, it isn't.

If there is one main take away from this post: always test and measure your code. Never trust, only test. Unexpected things may happen, and results may change over time. It's the same thing I've been saying since the first article. And it bears repeating because not enough people do this. You can inspect assembly, reduce branches, get rid of loops, use faster RNGs, etc. But all of that can go out the window if runtime was never recorded and compared.

Remember, the compiler will always be smarter than you and optimizations are wizard magic that we don't deserve.